Torsion (dihedral) functions

Dihedral functions are introduced to account for energy differences due to steric hindrance between atoms 1 and 4 when they are rotated about the 2-3 bond.

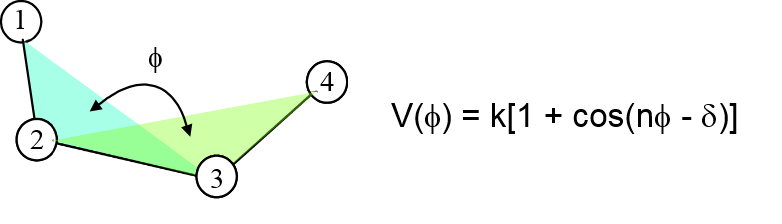
Cosine torsion (dihedral) potential about 2-3 bond.

where \(k\) is the torsion barrier, \(n\) is the periodicity and \(\delta\) is the phase shift.

By setting \(n = 3\), \(\delta = 0^{\circ}\), you can model the cis and gauche conformations between the hydrogen atoms in ethane, as shown below.

Cis and gauche effects in ethane associated with maximum and minimum torsion energies.

The cis conformation has the highest energy, whereas the gauche conformation has the least since the hydrogen atoms are the furtherest distance apart from one another. Note that there is no explicit trans conformation for ethane since there is only one type of atom (hydrogen) involved.

Note

The value of \(k\) is arbitrarily set to 2.0, representing the extent of energy differences between the two conformations (the well depth).

../../_images/Orange_bar2.png

For more complicated structures, one would need to model all different conformations with different energies. This can be achieved by expanding the dihedral function with additional terms, each with a unique contribution to the rotational energy:

\[V (\phi) = k_1 \left[1 + \cos \left(\phi - \delta_1 \right)\right] + k_2 \left[1 + \cos \left(2\phi - \delta_2 \right)\right] + k_3 \left[1 + \cos \left(3 \phi - \delta_3 \right)\right]\]

For example, for OPLS FF, the dihedral parameters for the general C-C-C-C group in an alkane chain are as follows:

  • \(k_1 = 1.135\) kcal/mol
  • \(k_2 = -0.151\) kcal/mol
  • \(k_3 = 0.4\) kcal/mol
  • \(\delta_1 = \delta_2 = \delta_3 = 0^{\circ}\)

The graph for this dihedral function is shown below:

Cis, gauche and trans effects in butane.

The structures shown on the right illustrate the rotation of terminal methyl groups in butane and the various conformations that result.

Note

The gauche conformation appears to be more stable than the trans conformation. While this is not the case for butane, the dihedral parameter sets were derived over a large number of test molecules with different atoms attached to the 1-4 positions. The parameters are therefore applicable, in a ‘general sense’, to molecules that contain alkyl chains. Bear in mind as well that there are other dihedral and other energy components that contribute to the structure of a molecule.

^ GO TO TOP ^