Lennard-Jones 12-6 Functions

The Lennard-Jones 12-6 function is the most commonly used function for vdW interactions due to its simplistic form for computation. It is expressed in various equivalent forms and they can be interchanged via algebraic operations.

\[V \left(r \right) = 4 \epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right]\]

\[V \left(r \right) = \epsilon \left[ \left(\frac{R}{r}\right)^{12} - 2 \left(\frac{R}{r}\right)^{6} \right]\]

\[V \left(r \right) = \frac{A}{r^{12}} - \frac{B}{r^{6}}\]

where \(\epsilon\) is the well depth measuring the strength of the interaction and \(\sigma\) is the steric parameter, which is the distance when the LJ function changes sign (when \(V = 0\)). \(R\) is the distance at which \(V\) is at its minimum value. These parameters are related to each other as follows:

\[R = 2^{ \frac{1}{6}} \sigma\]

The third form of the function is normally used in programming since it is easier to compute, with \(A\) and \(B\) having the following relationships:

\[A = 4 \epsilon \sigma^{12}\]

\[B = 4 \epsilon \sigma^{6}\]

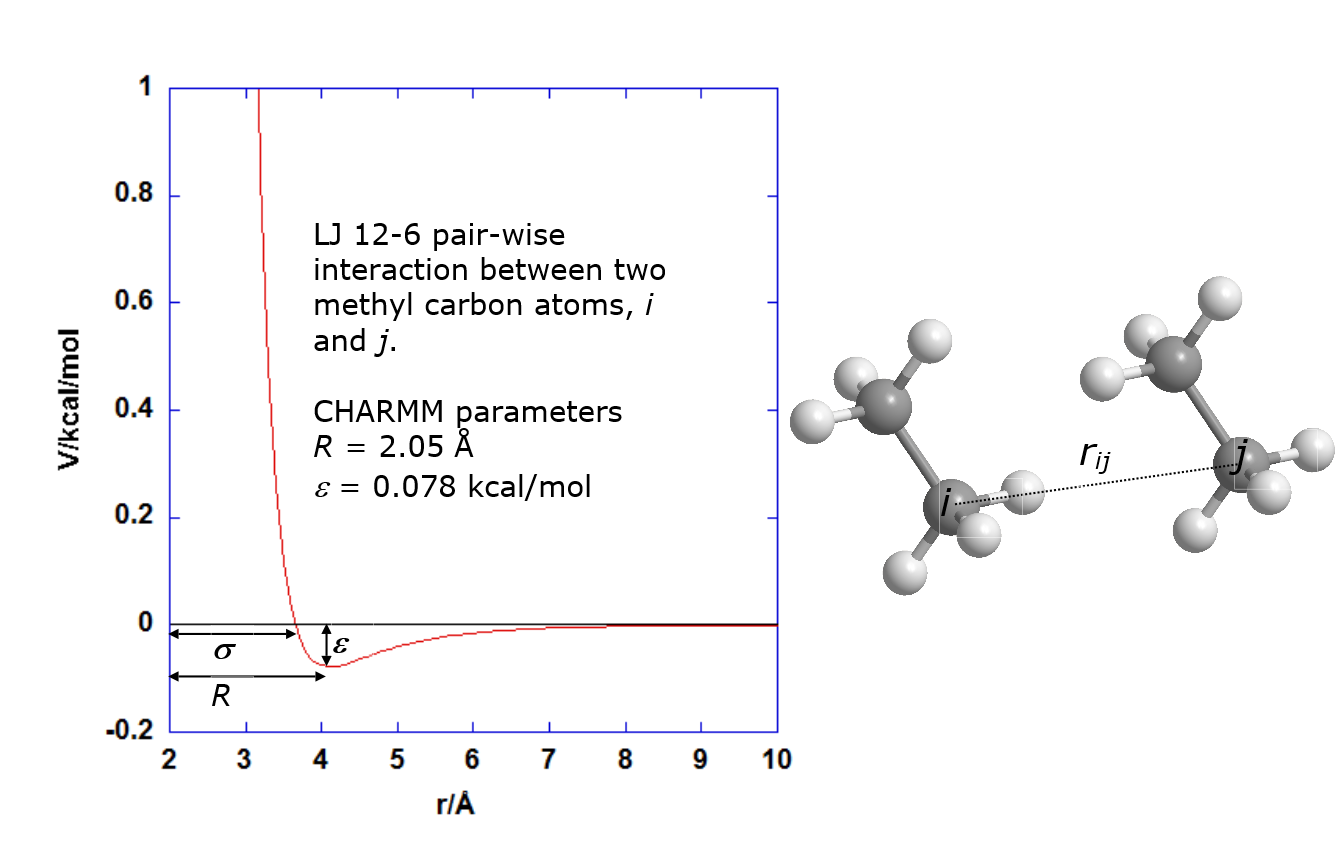
The diagram below shows the vdW interactions between two methyl carbon atoms with parameters obtained from the CHARMM FF.

^ GO TO TOP ^