Distance cutoffs and Ewald sums¶
Recall that non-bonded interactions are determined by summing up all possible pairs of atoms in the system. Quite often this is not feasible, and indeed, calculation of pairwise interactions is one of the major bottlenecks in molecular simulations.
In practice, only the atoms that are within a certain distance, called the cutoff distance, \(r_{cut}\), are considered in the calculations. All pairs more than \(r_{cut}\) apart will be ignored.
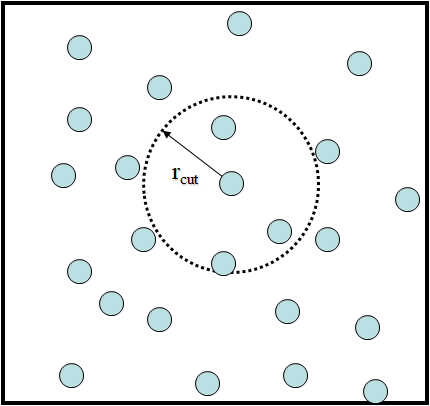

Cutoffs in vdW interactions
The LJ potentials decay (in \(\sim r^{-6}\)) asymptotically to zero at large distances. Simply ignoring the potentials beyond the \(r_{cut}\) will introduce a discontinuity in the force calculations and may introduce strange behaviour in the dynamics.
However, this behaviour may be negligible if \(r_{cut}\) is sufficiently large. In practice, \(r_{cut}\) is set to 10-15 angstroms. There are different ways to minimise the discontinuity:
Use of some sort of long-range correction, assuming a uniform density in the system.
Shift the whole function to zero at \(r_{cut}\). This is simple and convenient but it might alter the chemistry, considering that the well depth has also been shifted correspondingly.
Use of a smoothing function. This function would normally activate around \(r_{cut}\) and naturally smooth the function to zero at \(r_{max}\). For example, the use of a sine smoothing function with the following conditions:
\[\begin{split}f_c (r) = \begin{cases}1 & r \leq R-D \\ \frac{1}{2}-\frac{1}{2} \sin \left\{ \frac{\pi}{2} \left(r-R\right)/D \right\} & R-D < r \leq R+D \\ 0 & r \geq R+D\end{cases}\end{split}\]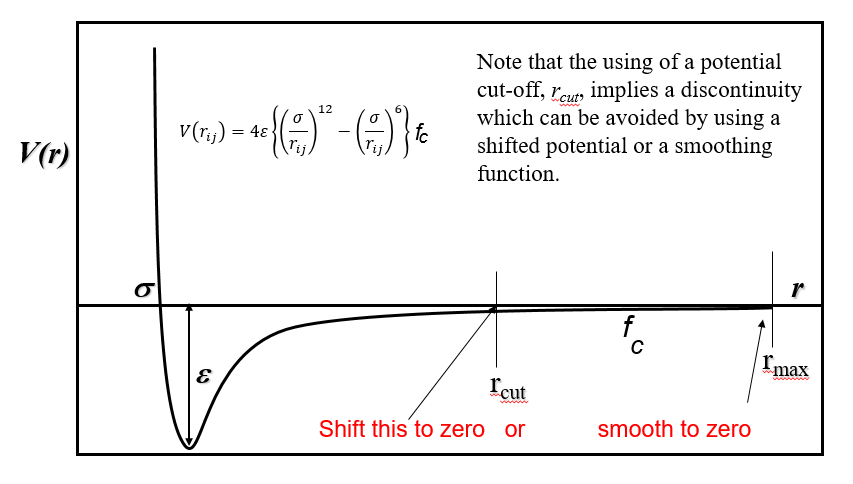
Note
For molecular systems with periodic boundary conditions, the value of \(r_{cut}\) set must not be larger than half of the length of the smallest box dimension. Otherwise, the minimum image convention cannot be applied to determine the distances between pairs of atoms for potential and force calculations.

Cutoffs in electrostatic calculations
Unlike LJ functions, the Coulombic function decays as \(r^{-1}\) so the discontinuity when truncating at \(r_{cut}\) would be more pronounced even at large distances. In addition, the decay is also conditionally convergent, and the results will depend on the order of summation. This means the usual cutoff tricks for vdW interactions cannot be applied and, in periodic systems, all charges would need to include periodic images.
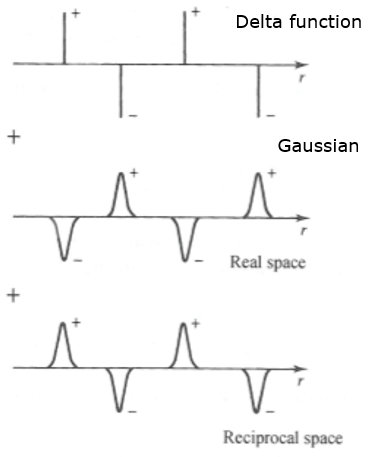
One way to solve this to use Ewald summation. This method converts the summations so they converge rapidly and absolutely in Fourier (reciprocal) space.
It offers a solution to solve the full electrostatic problem by splitting it into two parts: one in real space and the other in the reciprocal space.
In real space, complying with the usual cutoff concept, a convenient screening function (a Gaussian charge cloud) is added around all (delta-like) charges of opposite signs to make their interaction decay very quickly at \(r_{cut}\).
The added screening functions can then be subtracted in reciprocal space due to periodic boundary conditions by using Fourier transforms.
Finally, the completed Ewald sum requires an additional correction, known as the self-energy correction, which is a constant that arises from a Gaussian acting on its own site.
In summary, Ewald’s method replaces a potentially infinite sum in real space by two finite sums - one in real space, one in reciprocal space - and the self-energy correction. The precision of the Ewald sum is controlled by three parameters: \(r_{cut}\), a convergence parameter \(\alpha\) (related to the size of the Gaussian charge cloud) and the largest reciprocal space vector, \(k_{max}\).
| TIP: | In DL_POLY, the three Ewald parameters can be automatically determined by using the following directive in the CONTROL file:
or the equivalent for DL_POLY_5:
The quickest check on the accuracy of the Ewald sum is to compare the Coulombic energy (\(U\)) and its virial (\(v\)), which are shown in the OUTPUT or STATIS files. If the Ewald sum is sufficiently accurate, \(U = -v\). |
|---|